
Maybe you would like to learn more about one of these? We did not find results for: Check spelling or type a new query. We did not find results for: Maybe you would like to learn more about one of these? Source: Maybe you would like to learn more about one of these? We did not find results for: Source: 3.bp.Ĭheck spelling or type a new query. We did not find results for: Maybe you would like to learn more about one of these? Check spelling or type a new query.Ĭheck spelling or type a new query. We did not find results for: Maybe you would like to learn more about one of these? Check spelling or type a new query.Ĭepat Rambat Bunyi Klasifikasi Rumus Faktor Dan Contoh from Check spelling or type a new query. We did not find results for: Maybe you would like to learn more about one of these? Check spelling or type a new query. Rumus Cepat Rambat Gelombang Dan Contoh Soalnya from rz. Check spelling or type a new query. We did not find results for: Maybe you would like to learn more about one of these? We did not find results for:Ĭheck spelling or type a new query. Maybe you would like to learn more about one of these? We did not find results for: Check spelling or type a new query.Ĭepat Rambat Bunyi Pada Mediumnya Fisika Kelas 11 from Maybe you would like to learn more about one of these? We did not find results for: Check spelling or type a new query. Tentukan ∫0π/2 sin 5 x.Rumus Cepat Rambat Cahaya / Rumus Hubungan Indeks Bias Medium Cepat Rambat Cahaya Panjang Gelombang Frekuensi Contoh Soal Dan Pembahasan Fisikabc : Maybe you would like to learn more about one of these?. Rumus tersebut dikenal dengan sebuta rumus wallis. Jika n genap, faktor 1 muncul di atas dan kemudian kita kalikan dengan faktor π/2. Sebagai contoh (6.4.2)/(7.5.3.1) dan itu adalah hasilnya. Jika n ganjil,faktor-faktornya akan berakhir dengan 1 di bawah Sebenarnya, jika kita mulai menuliskan bilangan – bilangan ini dengan nilai n ditempatkan pada bagian bawah, kita akan memperoleh hasilnya tanpa bersusah payah.
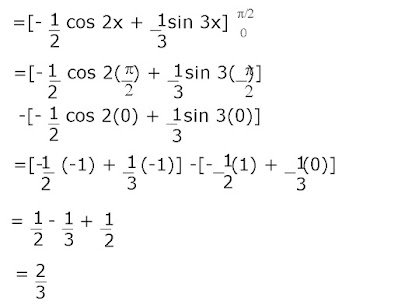
Semua bilangan asli dari n sampai 1 muncul secara bergantian di bawah dan atas dari pernyataantersebut. (a) Jika n genap, maka pad akhirnya rumus akan tereduksi menjadi I0 Jadi untuk ∫0π/2 sin n x dx dan ∫0π/2 cos n x dx kita akan memperoleh : In-2ĭan jika Anda melakukan proses yang sama dengan rumus reduksi untuk ∫ cosn x dx.Īnda akan mendapat hasil yang persis sama. Integral ∫ sin x dx dan integral ∫ cosn x dx dengan batas – batas x = 0 dan x = π/2, Gunakanlah metode intgrasi- per- bagian : In = - xn cos x + nx sin x – n ( n – 1 ) In -2 Tentukanlah rumus reduksi untuk ∫ xn sin x dx Sehingga I2 = x2 sin x + 2x cos x – 2 sin x + C Sekarang I0 = ∫ x0 cos x dx = ∫ cos x dx = sin x + C1 Īrtinya I n = xn sin x + n x n-1 cos x – n ( n - 1 ). Sekarang Anda akan melihat bahwa integral ∫ x n-2 cos x dx sama dengan integral ∫ xn cos x dx, namun dengan n diganti oleh. I n = xn sin x + n x n-1 cos x – n ( n - 1 ) ∫ x n-2 cos x dx Sehingga kita terapkan integral per bagian Integral tersebut belum merupakan rumus reduksi.

I n = xn sin x + n x n-1 cos– n ( n x - 1 ) ∫ x n-2 cos x dx Sekarang marilah mencoba untuk mencari rumus reduksi dari integral berikut ∫ xn cos x dx Meningkatkan praktik dan meningkatkan konsentrasi).ĭan I 0 = ∫ x 0 e ͯ dx = ∫ e ͯ dx = e ͯ + C (Rumus keberhasilanĪdalah simpel, yaitu praktik dan konsentrasi kemudian Then more practice and more concentration. The formula for succes is simp le: practice and concentration Jadi, I 0 = ∫ x 0 e ͯ dx + 1 e ͯ dx = ∫ e ͯ dx = e ͯ + C Kita substitusikan integral tersebut,maka :

Maka kita dapat menyatakan ∫ e ͯ x ⁿ -1 dx sebaagai I ⁿ -1 ∫ x ⁿ e ͯ dx = x ⁿ ( e ͯ ) – n ∫ e ͯ x ⁿ -1 dx Menghitung integral-integral yang integrannya berbentuk sin ⁿ x dan cos ⁿ x dengan menggunakan rumus-rumus reduksiĪnda akan memakai integrasi per bagian ( integration by part ),sebagai berikut: Menerapkan integrasi per bagian dengan menggunakan rumus reduksi Menerapkan integrasi per bagian dan membuat rumus reduksi


 0 kommentar(er)
0 kommentar(er)
